“233 coppie di conigli” rispose, per primo, Leonardo Pisano.
Pisa, Anno Domini 1223. L’imperatore Federico II di Svevia, presente al torneo tra abacisti e algoritmisti, sta per constatare che il metodo posizionale indiano riferito dagli arabi avrebbe permesso di calcolare ogni soluzione più velocemente di qualsiasi abaco. Il problema: «un certo uomo mette una coppia di conigli in un posto circondato su tutti i lati da un muro. Quante coppie di conigli possono essere prodotte da quella coppia in un anno, se si suppone che ogni mese ogni coppia genera una nuova coppia, che dal secondo mese in avanti diventa produttiva?».
Leonardo, detto Bigollo, conosciuto anche come “fillio Bonacci” o Fibonacci, visse in Oriente e fu educato dai Maestri di Algeri, viaggiò in Siria, Egitto e Grecia e conobbe numerosi matematici musulmani. La sua conoscenza si riversò nel monumentale Liber Abaci, passato alla storia per la descrizione inedita di quel segno sconosciuto all’Occidente e trascritto come zefito, zefr, o zero, ovvero un numero vuoto come un soffio di vento: quod arabice zephirum appellantur.
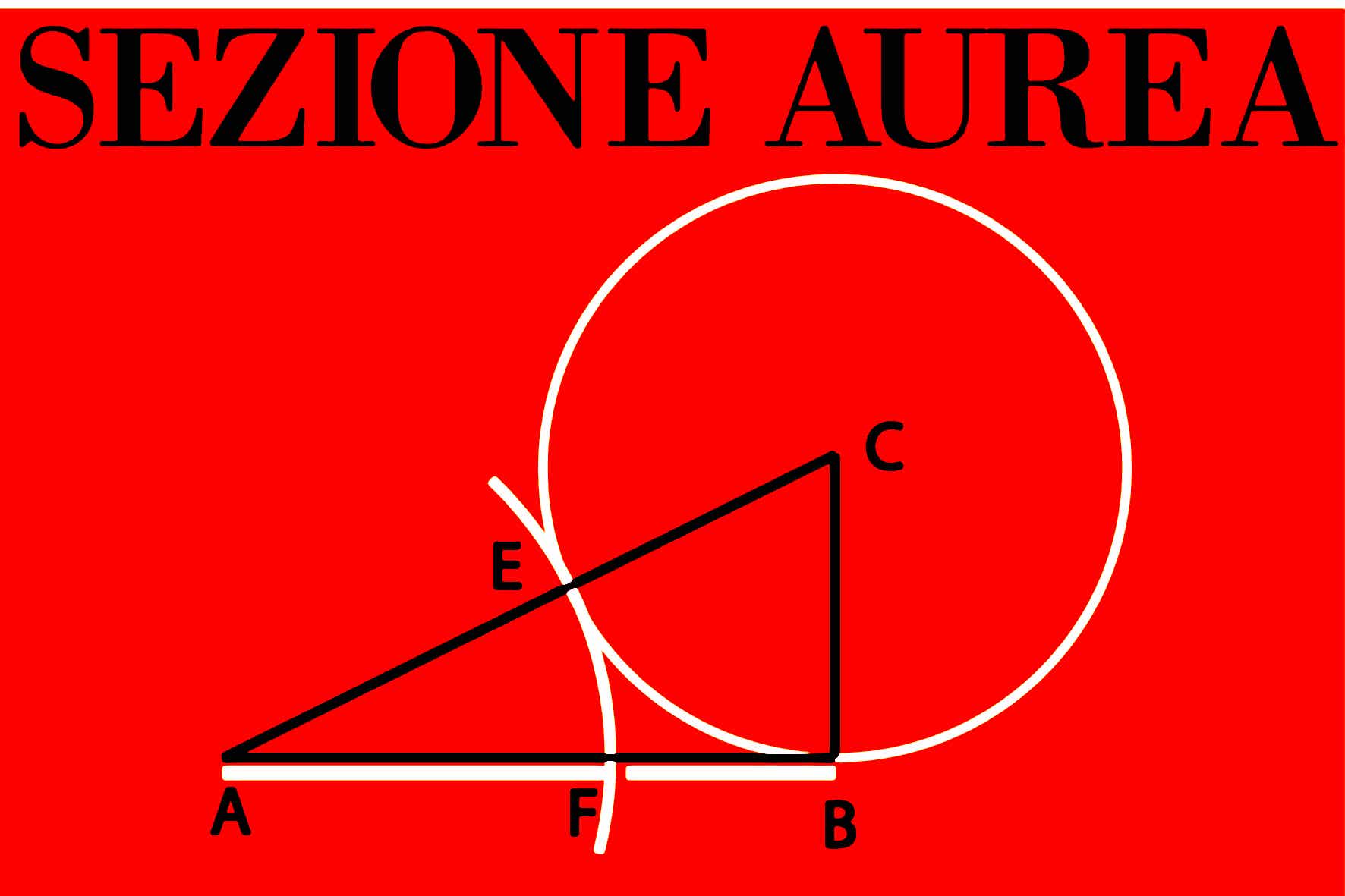
Correlata alla successione di Fibonacci è la sezione aurea, quella lunga serie di cifre decimali aperiodiche riassunte nel φ (phi), ma che risultano facilmente rappresentabili geometricamente: ed ecco i rettangoli di Fibonacci, il triangolo aureo, la spirale logaritmica… ”Tutto è numero” esclamava Pitagora e se tale rapporto aureo è parte integrale della piramide di Giza, dei megaliti di Stonehenge, della Cattedrale di Nôtre Dame a Parigi o del Palazzo dell’ONU a New York tale proporzione non mancò nella scultura di Fidia o nei dipinti di Leonardo da Vinci che pitturava la bellezza del volto di Monna Lisa applicando tale regola alle proporzioni del suo viso.
I numeri di Fibonacci li ritroviamo anche nella musica e in talune composizioni, ma è la natura, che ripetendo tale armonia, stimola l’istinto che forza la curiosità: il rapporto aureo è difatti presente nelle distanze armoniche dei pianeti dal Sole. Nel 1509 a Venezia, il matematico Luca Pacioli diede alle stampe il suo De divina Proportione, illustrato con disegni di Leonardo Da Vinci, e si divinizzò ciò che già era ritenuto universalmente aureo.
La costante è un numero matematicamente irrazionale. Fibonacci l’ha chiarito, espresso, constatato, descritto, pubblicato.
Qui, tuttavia, ci si interessa di cibo, di gastronomia e di cucine, perché l’atto del mangiare è nell’animale umano un istinto culturale prima ancora di essere una necessità fisiologica. Brillat-Savarin diceva che “la gastronomia è la coscienza di tutto ciò tutto ciò che si riferisce all’uomo in quanto essere che si nutre” e se attorno a questo fatto sociale totale, a detta del semiologo Roland Barthes, è lecito convocare vari metalinguaggi (la fisiologia, la chimica, la geografia, la storia, l’economia, la sociologia e la politica), mi sento in diritto di invitare il linguaggio dei numeri.

Sostengo difatti che, in alcuni casi eccellenti, in cucina si generi una divina proporzione.
I fattori generativi sono molti, complessi e difficilmente catalogabili, di contro la natura che li caratterizza pare riconducibile allo stato di costanza o di variabilità. La creatività che i cuochi effondono nella preparazione di ricette è propria della variabilità, e ciò non preclude alcun approccio di studio o tentativi di teorizzazione dei suoi principi motori.
Federico Ruggero Costantino di Hohenstaufen, già Re di Sicilia, Duca di Svevia e Re dei Romani, in qualità di Imperatore del Sacro Romano Impero e poco prima di essere incoronato Re di Gerusalemme, non tardò molto a redigere quel che il motto Ad Scientiarum Haustum et Seminarium Doctrinarum riassume con equa riflessione e franca dignità, così che i digiuni e gli affamati di sapere trovino di che soddisfare le proprie brame e non siano costretti, per ricercare la conoscenza, a peregrinare e a mendicare in terra straniera.








Commenti